FLATlandia
"Abbi pazienza, ché il mondo è vasto e largo" (Edwin A. Abbott)

---------

Commento

Abbiamo ricevuto tre risposte, tutte da classi seconde di Licei Scientifici.

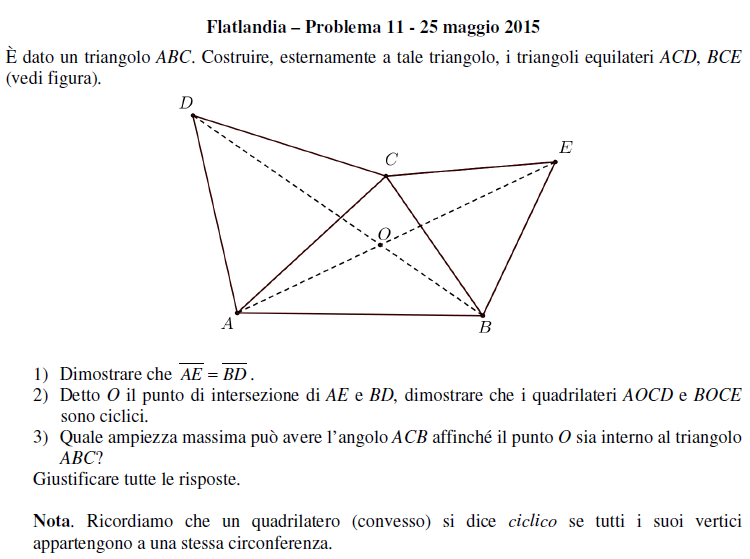
Il problema poneva tre quesiti tutti relativi a una stessa figura costituita da un triangolo su due lati del quale erano costruiti esternamente due triangoli equilateri, i cui vertici liberi venivano poi congiunti con gli estremi opposti del terzo lato del triangolo iniziale.  Si chiedeva  di dimostrare tre diverse proprietà geometriche, e precisamente:

1) che i due segmenti costruiti come descritto erano congruenti;

2) che i due quadrilateri aventi come vertici i vertici di uno dei due triangoli equilateri costruiti e il punto di intersezione dei segmenti predetti erano ciclici;

3) determinare l’ampiezza massima dell’angolo avente come vertice il vertice comune ai due lati su cui erano stati costruiti i due triangoli equilateri, affinché la predetta costruzione fosse possibile.

In una sola delle risposte pervenute il problema viene risolto in tutte le sue parti in modo sufficientemente corretto. In una seconda risposta mancano spesso le motivazioni per certe proprietà geometriche usate. Infine nella terza risposta la costante confusione tra un ente geometrico e la sua misura arriva al punto di stabilire la congruenza tra un angolo e la sua ampiezza.

Sono pervenute risposte dalle seguenti scuole:

• LS “A. Volta”, Colle di Val d’Elsa (SI)

• LS “Aristosseno”, Taranto (TA)

• LS “U. Dini”, Pisa (PI)

Come di consueto presentiamo tutti i commenti riuniti in questo unico file pdf  (richiede Acrobat Reader).
NOTA. Nelle soluzioni riportate, le correzioni, le aggiunte o i commenti sono scritti fra parentesi quadre.
Con doppia parentesi quadra vengono indicate le parti omesse.

Il gruppo di lavoro che gestisce FLATlandia :

- Ercole Castagnola, NRD Università di Napoli “Federico II”

- Giuliano Mazzanti, Docente di Geometria, Università di Ferrara

- Valter Roselli, Ricercatore, Dipartimento di Matematica, Università di Ferrara

- Luigi Tomasi, Insegnante di Matematica, Università di Ferrara

| Home Page Cabri | Torna a FLATlandia | Archivi |