L'attività qui descritta è stata svolta nella classe 1 D del Liceo Issel il 17 dicembre 2001 ed è durata 2 ore. Si trattava della seconda esperienza con i sensori di movimento, strumenti particolari che consentono di rilevare la posizione di un corpo in moto. Collegandoli a una calcolatrice in grado di elaborare numericamente e graficamente i dati ricevuti, è possibile proiettare su uno schermo la traccia della legge oraria della posizione al variare del tempo, ma anche quella della velocità e, seppure con qualche problema, quello dell'accelerazione. La prima esperienza con l'uso dei sensori si era svolta quasi due mesi prima. La lezione è stata videoregistrata e analizzata da un'osservatrice, Silvia, laureanda in matematica, che ha seguito le lezioni per una trentina di ore. Qui di seguito riportiamo l'introduzione all'attività da parte dell'insegnante e le osservazioni di Silvia sullo svolgimento dell'attività. Facciamo notare che osservazioni così analitiche sull'attività che si è svolta in classe sono particolarmente utili all'insegnante per valutare, nel tempo, l'efficacia del suo operato. Possedere un elevato numero di osservazioni di questo tipo consente di avere informazioni sui processi attivati dagli studenti e sull'evoluzione del loro percorso molto più significative di quelle consentite da una prova tradizionale. In questo senso le prove tradizionali perdono significato, in una didattica di questo tipo: infatti sono molto meno significative delle osservazioni analitiche che, in quest'esperienza, sono state accompagnate anche da videoregistrazioni. La videoregistrazione è poi stata fatta rivedere agli studenti, circa quindici giorni dopo, per analizzare il comportamento poco redditizio in una discussione di alcuni studenti che sono intervenuti parecchie volte, ma senza prestare attenzione agli interventi dei compagni.
L'introduzione all'attività da parte dell'insegnante
Come vi ricorderete, abbiamo già effettuato una prima esperienza con il sensore di moto; tutti tranne Beatrice. Oggi torniamo a lavorare con il sensore di moto. La prima attività che faremo sarà molto simile a quelle già viste. In questo modo cercheremo sia di rinfrescare quell’esperienza, sia di consentire a Beatrice di effettuarla direttamente almeno una volta, visto che la vola precedente era assente.
È necessario svolgere queste attività in modo ordinato, senza alcuna confusione, perché i concetti che dobbiamo affrontare oggi sono particolarmente delicati e richiedono la massima concentrazione. Alla fine di ogni prova ciascuno di voi potrà chiedere eventuali chiarimenti pubblicamente. In alcuni casi darò una risposta immediata, in altri potrei richiedere a tutti di partecipare alla discussione: ricordatevi che sarò io a condurre la discussione e dovrete prestare molta attenzione a non intervenire in modo incontrollato.
Chiederemo poi al prof. di fisica di preparare una prova scritta relativa a concetti della cinematica.
Attività 1.
Io disegnerò alla lavagna una traccia distanza – tempo e ciascun coordinatore dovrà muoversi in modo che la calcolatrice riproduca la traccia disegnata sullo schermo. Alla fine di ciascuna prova, i componenti del gruppo del coordinatore che si è mosso, potranno correggere eventuali errori del compagno. La correzione andrà effettuata prima verbalmente e poi riproducendo un grafico più simile a quello disegnato. Tutti gli altri studenti dovranno stare particolarmente attenti a questa attività, cercando di capire in che modo sono legate la velocità del corpo che si sta muovendo e la sua accelerazione alle caratteristiche del grafico. Infatti l’attività di oggi è finalizzata proprio a scoprire, alla fine, come accelerazione e velocità sono legate alle caratteristiche del grafico distanza – tempo. I coordinatori dei gruppi oggi sono: Mattia, Gian Luca, Cristina, Lucrezia, Beatrice.
Attività 2.
I quattro studenti (di gruppi diversi) che hanno effettuato le migliori prestazioni nella precedente attività dovranno muoversi rispetto al sensore, senza guardare il grafico proiettato sul muro e dire che tipo di grafico si produce in conseguenza del loro movimento. I due compagni di gruppo dovranno, alla fine della prova, individuare eventuali errori e dare indicazioni di come si sarebbero potuti evitare (ossia devono dire come avrebbe dovuto muoversi il loro compagno).
Attività 3.
La calcolatrice consente di disegnare anche i grafici della velocità e dell’accelerazione (anche se meno precisi di quello della distanza). Uno studente per ciascun gruppo si muoverà rispetto al sensore e ogni volta confronteremo il grafico distanza – tempo con quello velocità – tempo. Ciascun gruppo dovrà cercare di rispondere alla domanda “che relazione c’è tra i due grafici?” Avendo il grafico della “distanza – tempo” sono in grado di determinare quello della velocità? E il viceversa?
Ciascun gruppo che ha la necessità di fare altre prove deve spiegare esattamente quale congettura intende verificare
Attività 4.
Uno studente di ciascun gruppo si muove rispetto al sensore e, aiutato dai compagni di gruppo dovrà disegnare alla lavagna il grafico della velocità – tempo corrispondente al suo movimento.
Attività 5.
Io mi muoverò rispetto al sensore e poi raccoglieremo, con la funzione “trace”, una quarantina di dati (distanza – tempo) che elaboreremo in classe nelle prossime lezioni, cercando di capire in che modo essi possono darmi informazioni sulla velocità del corpo e quale interpretazione geometrica ha la velocità di un corpo.
In generale, cercheremo di capire che relazione esiste tra la variazione di una grandezza e la velocità con cui varia quella grandezza.
Osservazioni di Silvia (in nero vengono riportati dialoghi e fatti così come si sono svolti; in rosso i commenti di Silvia e in viola i successivi commenti dell'insegnante dopo aver rivisto il video a casa)
La
lezione odierna è caratterizzata dall’ utilizzo dei sensori di moto come
mezzo per giungere a una corretta interpretazione dei legami funzionali, fra
grandezze come spazio, tempo, velocità e accelerazione.
Il professore presenta l’
esperienza:
“ Questo è un congegno che
consente di rilevare le posizioni di un oggetto che è in movimento, al variare
del tempo,” intanto si posiziona davanti al sensore e muove la mano avanti e
indietro perpendicolarmente allo strumento, “ per esempio, in questa posizione
lo strumento rileverebbe una distanza rispetto a lui di 1 m a un certo istante
di tempo. Se io mi muovo,” e fa un passo avanti, “ ottengo un grafico della
mia posizione, o meglio della mia distanza rispetto a questo oggetto,” indica
il sensore, “ al variare del tempo. Ci sono relazioni difficili che legano
spazio, velocità, tempo e accelerazione e noi dobbiamo cercare di
approfondirle.”
Il modo di esprimersi del
professore, con un ampio utilizzo della gestualità, è un preambolo importante
all’ uso marcato che di questo parametro sarà fatto nell’ arco dell’
esperienza. Il linguaggio dei gesti è ancora indispensabile alla comunicazione
per sopperire alle molte lacune del linguaggio, ed in particolare alla sua
funzione di chiarimento.
ATTIVITA’ 1
PROF: “ Io disegnerò alla lavagna un grafico del tipo
distanza-tempo,” traccia gli assi cartesiani, “ogni coordinatore dovrà
muoversi in modo che la calcolatrice riproduca la curva disegnata sulla lavagna.
Gli altri componenti del gruppo potranno correggere eventuali errori del
coordinatore. Lo scopo dell’ esperienza è di fare delle congetture per capire
come sono legate la velocità, e magari l’ accelerazione, che è una
variazione di velocità, alla forma del grafico distanza-tempo.”
Espressione della funzione
contrattuale del linguaggio.
Il
primo studente ad essere interpellato è Mattia, a cui si chiede di riprodurre
il seguente grafico (distanza – tempo)
![]() d
d
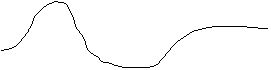
Mattia
parte da metà aula, va indietro piano, avanti velocemente, torna indietro e si
ferma più e meno nel punto da cui era partito inizialmente. Terminata l’
esperienza, non sembra però molto soddisfatto del risultato ottenuto.
Il
professore chiede ai compagni di gruppo di intervenire.
Irene:
“ Forse doveva andare più veloce subito.”
Erik: “ Cioè prima piano, poi veloce,” e alza la mano
come per buttarsi rapidamente qualcosa alle spalle, “ poi veloce giù,”
abbassa la mano, “poi rallentare” e descrive con la mano una curva concava
discendente, “poi veloce di nuovo.”
Manifestazione della funzione
programmatrice del linguaggio verbale, coadiuvata dall’ utilizzo delle
funzioni contrattuale e di chiarimento del linguaggio gestuale.
PROF: “ Erik, tu pensi di poter far meglio? Perché
no?”
Irene:
“ Perché è fatto abbastanza bene!”
PROF:
“ Quindi quelli che ha dato Erik sono solo suggerimenti teorici.”
Irene: “ Sì, è solo questione di velocità.”
Irene trova un primo ponte di
collegamento fra grafico distanza-tempo e velocità, che potrebbe produrre un
avanzamento in zona di sviluppo prossimale in lei e nei compagni, ma che non
viene percepito.
Va
alla lavagna Gianluca, a cui viene proposto il seguente grafico.
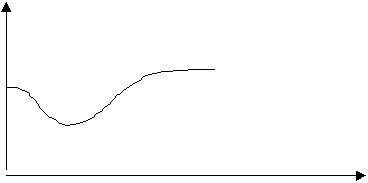
Il
ragazzo parte dal fondo della classe, si muove in avanti velocemente e torna
indietro sempre velocemente, poi si ferma.
Alessio: “ Ti sei avvicinato troppo e dovevi stare più
fermo all’ inizio, invece il tuo grafico fa subito così,” e muove
rapidamente la mano diagonalmente verso il basso.
Le funzioni contrattuale e di
chiarimento sono chiaramente coadiuvate dall’ utilizzo dei gesti.
Stefano pensa di poter ottenere un risultato migliore
partendo più velocemente. Tenta, ma il prodotto non è
soddisfacente, tutta la classe ne conviene.
La calcolatrice e il sensore sono
sfruttati come strumenti di validazione.
Alessio
ribadisce, quindi, la sua ipotesi.
Michele:
“ Sì, perché quella curva vuol dire che prima parte piano e poi accelera.”
PROF:
“ Alessio come fai a capire che parte piano?”
Alessio: “ Basta vedere che non fa così,” e ripete il
movimento di prima con la mano, “ ma fa così,” e descrive la curva della
lavagna.
Grazie all’ azione in zona di
sviluppo prossimale del professore, Alessio riesce a chiarire la sua deduzione,
frutto di una dinamica interno/esterno nata dal confronto fra i due segni
grafici prodotti.
Stefano: “ Però all’inizio non si sa quanto deve
rimanere fermo.”
Il concetto di grafico è
strettamente connesso a quello di assi cartesiani e di unità di misura. In
questo caso, tali campi concettuali adiacenti non sono comunque cruciali, è
quindi necessario l’ intervento del professore per focalizzare e consolidare
il fulcro del discorso.
PROF:
“ Sì, è vero, perché non abbiamo dato una scala per l’ asse dei tempi, ma
sappiamo che l’ esperienza dura circa 13 secondi, allora possiamo pensare l’
asse dei tempi diviso in 13 parti uguali. Comunque ci siamo resi conto che
questa,” e indica la prima porzione del grafico, “ come la chiamiamo?”
Suggeriscono
curvatura, pendenza, cunetta.
Siamo di fronte ad un avanzamento
in zona di sviluppo prossimale, come manifesta la poca padronanza della
terminologia: non è noto un nome specifico per indicare il nuovo oggetto
scoperto.
PROF:
“ Che questa curvatura, pendenza, cunetta è lieve inizialmente, quasi nulla,
e questo è associato alla velocità iniziale.”
E’
il turno di Cristina che deve riprodurre la curva…
Parte da metà aula, indietreggia velocemente, si ferma,
avanza rapidamente e si riferma.
Francesco:
“ Secondo me all’ inizio doveva partire un po’ prima e fare in modo che
quel tratto fosse un po’ più corto,” per indicare il trattino utilizza
pollice e indice, che vengono disposti a formare una c.
Michele:
“ Io sarei partito un po’ più indietro.”
La manifestazione di una dinamica
interno/esterno a partire dal grafico prodotto da Cristina, porta Michele ad una
congettura. Tutto ciò consente al professore un’ azione in zona di sviluppo
prossimale: le ipotesi prodotte vanno validate e la calcolatrice ed il sensore
possono essere utilizzati a tale scopo.
PROF: “ Quindi è la posizione di partenza che non
funziona, ma la macchina mostra che la posizione di Cristina dista da quella di
partenza solo di pochi cm.”
Paola:
“ No, secondo me doveva andare più velocemente quando è tornata avanti,
quando è tornata verso il sensore.”
Secondo
Alessio questo problema è legato ancora alla posizione di partenza. Gianluca
non è d’ accordo, Alessio si corregge: non è la posizione di partenza il
nodo fondamentale, ma il tempo e prova a riprodurre la traccia, per avvalorare
la sua ipotesi e spiegare quello che non riesce a dire a parole. Non ottiene però
un risultato significativo.
Il movimento, gli strumenti e il
grafico come mezzo di comunicazione.
Francesco
sostiene che forse l’ unico modo per migliorare il grafico di Cristina è di
rallentare sempre di più mentre si torna indietro.
PROF: “ Il problema è solo di asimmetria: a sinistra
sale troppo velocemente e a destra scende troppo lentamente.”
Intervento di chiarimento e
riferimento al campo concettuale simmetria.
Va
alla lavagna Carlotta, che deve riprodurre questo grafico:
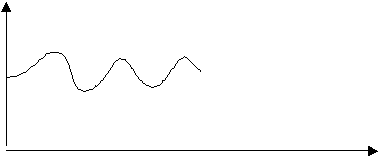
Si
muove avanti e indietro rispetto al suo punto di partenza iniziale diverse
volte.
Simone:
“ E’ andata troppo lenta, perché non è riuscita a completare la serie.”
PROF: “ Che cosa doveva accelerare?” E muove la mano
avanti e indietro parallelamente al pavimento.
Azione in zona di sviluppo
prossimale, esercitata anche sfruttando il linguaggio gestuale, che può servire
come trampolino, e così avviene, per l’ attuazione di una dinamica
interno/esterno.
Gianluca:
“ Il movimento.”
Irene:
“ Doveva oscillare.”
PROF:
“ Quindi aumentare la velocità di oscillazione.”
Irene:
“ No, solo nella salita e nella discesa.”
Michele:
“ Doveva stare più ferma nel cambio di direzione.”
PROF:
“ Simone potresti provare a migliorare il grafico.”
Erik:
“ La prima ha fatto bene, perché si è fermata, poi ha fatto…” e vibra
velocemente la mano su e giù. Si parla di velocità della serie, velocità di
oscillazione, velocità di andare avanti e indietro
PROF: “ Avete mai sentito parlare di frequenza?”
Chiarimento in merito alla
terminologia.
ATTIVITA’ 2
Il
professore passa, quindi, a illustrare la seconda attività, che consiste nel
produrre un grafico dando le spalle al sensore, descrivendo verbalmente l’
andamento che si pensa avrà la curva così ottenuta: “ Va in salita, fa una
curva, la pendenza aumenta.”
Inizia
l’ esperienza Gianluca.
PROF: “ Pensa al movimento che vuoi fare e ricorda che
adesso,” intanto si allontana di schiena dal sensore, Gianluca: “ E’ al
contrario.”
Ancora il movimento come
linguaggio per comunicare.
PROF:
“ Ci devono essere almeno tre variazioni di andamento.”
Gianluca: “ Una linea orizzontale, sale piano, scende
velocemente, una linea orizzontale, sale, fermo.”
Espressione della funzione
logica.
PROF:
“ Non è descritto male.”
E’
il turno di Erik: “ Sale piano, veloce, fermo, scende piano, veloce, sale
piano, fermo.”
Va alla lavagna Carlotta: “Si abbassa piano, va
veloce,” intanto si muove in avanti, “ferma, si abbassa piano, ferma, si
alza piano, si ferma.”
E’
la volta di Beatrice: “ Si abbassa piano, si alza piano, sta fermo si abbassa
veloce, si alza piano, sta fermo.”
PROF: “ Sta fermo cosa
vuol dire?”
Beatrice:
“ Che c’è una linea orizzontale.”
PROF: “ Cioè la pendenza è ?”
Gianluca:
“ Zero.”
Azione in zona di sviluppo
prossimale.
Viene
interpellato Francesco: “ Mi alzo piano, mi fermo, torno indietro veloce, vado
su veloce, mi fermo.”
Il
professore fa notare l’ uso nel suo linguaggio di verbi riflessivi: la
descrizione doveva essere della curva, non del movimento fatto. Francesco si
corregge.
ATTIVITA’ 3
PROF: “ Ci siamo resi conto che nel muoversi nel tempo,
può variare la velocità e, conseguentemente, anche l’accelerazione, che è
una variazione di velocità. Se c’ è un tratto di retta la velocità cosa
fa?”
In coro: “ E’ costante.”
Espressione delle funzioni
contrattuale e di chiarimento: vengono riassunti e puntualizzati gli elementi
peculiari delle scoperte fatte.
Michele:
“ Ma non si riesce mai a disegnare delle rette, perché partiamo sempre da
fermi.”
Stefano: “ Potrei partire prima!”
Manifestazione di una dinamica
interno/esterno: Stefano riesce a produrre una congettura a partire da un
ragionamento di Michele. Tutto ciò consente al professore un intervento in zona
di sviluppo prossimale.
PROF:
“ Stefano suggerisce una partenza lanciata, cioè partire prima che il sensore
si azioni. E cosa succede quando mi fermo?”
Michele:
“ Decelera e la …” descrive una conca capovolta con la mano.
PROF:
“ Le calcolatrici consentono di misurare anche i grafici della velocità e
dell’ accelerazione. Ora produrremo dei grafici distanza-tempo e li
confronteremo con il grafico, che fornisce la calcolatrice, della velocità.
Dobbiamo cercare di capire che relazione c’ è fra le due curve.”
Stefano ritiene che la relazione sia connessa alla
definizione di velocità come rapporto fra spazio e tempo, per Gianluca, invece,
è da ricercarsi nello studio della pendenza delle curve.
La parola velocità produce degli
effetti diversi nei ragazzi: per Stefano è legata alla rappresentazione spazio
fratto tempo, per Gianluca, che progredisce in zona di sviluppo prossimale, al
concetto di pendenza.
PROF:
“ Perché?”
Gianluca:
“ Perché quando le curve sono molto ripide,” scende perpendicolarmente al
pavimento con la mano, “ si va veloce, se, invece, salgono poco, vuol dire che
siamo andati piano, lo abbiamo visto prima.”
Simone
pone un’obiezione al ragionamento di Stefano: “La velocità calcolata con la
formula è la velocità per un dato tempo, ma non è costante.”
Michele:
“ Comunque la velocità parte da zero!”
Erik:
“ No, parte dall’ asse delle velocità, se parte già veloce.”
Anche
se non è stato riportato, qui si apre una lunga discussione tra Michele ed Erik.
Michele vuole sostenere che la velocità “parte sempre da 0” e prende la
parola più volte, interrompendo spesso il discorso e non prestando attenzione
agli interventi degli altri. Il fatto di non prestare attenzione agli interventi
dei compagni è un po’ una caratteristica che emerge soprattutto in due
(lunghi) momenti del filmato, diciamo dalle ore 10.18 alle ore 11.03, con
Michele protagonista negativo. In due occasioni Michele sostiene alcune idee che
sono in aperta contraddizione con quel che si vede sul grafico o con quello che
effettivamente è accaduto in classe. Anche quando la contraddizione viene
esplicitata dall’insegnante, Michele continua a difendere la sua idea,
cercando di cambiare continuamente le premesse del proprio ragionamento.
PROF:
“ Vedremo.”
Il
“vedremo” dell’insegnante ha lo scopo di incitare i ragazzi a fare
esperimenti che possano confermare o confutare le ipotesi e le congetture
proprie e dei compagni. L’ideale sarebbe che una volta stabilite due ipotesi
contrastanti (come quelle di Erik e
Michele) si passasse alla verifica sperimentale. Invece gli studenti tendono a
discutere sulle ipotesi fatte, modificandole, introducendo altre complicazioni,
altre idee per convincere gli altri, ma senza riuscire ad essere ascoltati e
senza riuscire ad ascoltare i compagni. Si genera così un classico dialogo tra
sordi che solo l’azione continua dell’insegnante riesce a non fare
degenerare. Potrebbe essere interessante far rivedere agli studenti gli ultimi
trenta minuti di discussione (dalle 10.18 alle 11) e commentarli insieme.
Francesco:
“ Si vede anche dal numero di oscillazioni se sono maggiori…” (l’ ultimo
grafico descritto presenta alcune oscillazioni.)
PROF: “ Proviamo a vedere cosa succede, andiamo a
controllare.”
Invito a verificare
sperimentalmente le proprie congetture.
Viene
ripresa l’ idea della partenza lanciata, anche se Irene, che parlando distende
le braccia, sostiene che non è applicabile per via delle dimensioni della
stanza.
Quando l’insegnante propone
l’idea di guardare il grafico (s,t) per ottenere informazioni sul grafico
(v,t) Michele ritiene il problema inutile o banale, “basta applicare le
formule” (ridendo). L’insegnante deve riprendere più volte il filo del
discorso per far capire che non è detto che le formule (almeno quelle che gli
studenti conoscono) siano di immediata utilità per ricavare informazioni sul
grafico (v,t) a partire dal grafico (s,t).
Michele continua a considerare il
problema proposto banale, come suggerisce l’ espressione del suo viso, per via
delle relazioni formali esistenti fra le grandezze in gioco. Il professore
chiarisce, quindi, additando quello disegnato alla lavagna, che il centro del
discorso non è la relazione fra grandezze, ma fra grafici. Michele in risposta
produce una smorfia di disappunto, non vede la differenza fra le due diverse
consegne.
Michele non riesce a cogliere la
situazione problematica, neanche dopo il suggerimento del professore, forse
perché il concetto di grafico cartesiano, per lui, non rientra nell’ insieme
delle rappresentazioni possibili per il campo concettuale velocità.
PROF:
“ Se avete delle congetture, muovetevi in modo tale da verificarle o
confutarle.”
Altro
invito a passare alla sperimentazione per mettere ordine nella discussione.
Michele:
“ Se si parte la fermi, si accelera e ci si blocca, cosa succede? Il grafico
è una verticale,” e muove un dito su e giù perpendicolarmente al pavimento.
PROF:
“ Voi cosa ne pensate?”
Secondo
Irene: “ Va giù, perché ti fermi!”E scende con la mano.
Simone
chiede un chiarimento sulla disposizione delle grandezze in gioco sugli assi
cartesiani: “ Il tempo va messo per così?”Muove un braccio orizzontalmente
da sinistra verso destra.
Continua
a sussistere il problema di dove parte il grafico se l’ oggetto è
inizialmente fermo.
Irene
va alla lavagna. Si muove un po’ avanti un po’ in dietro, poi si ferma in
punto a una certa distanza dal sensore, torna indietro e riavanza, fermandosi
all’ incirca in quello stesso punto.
La
calcolatrice produce il grafico distanza-tempo.
PROF: “ Mentre viene elaborato il secondo grafico
cercate di immaginare come verrà fuori.”
Esplorazione della zona di
sviluppo prossimale.
Erik
prende subito la penna, sembra abbia capito e cerchi di non perdere l’
intuizione. Disegna questi due grafici:
Erik
e Mattia sono d’ accordo sul risultato ottenuto, invece Irene è contraria:
“Fa così lo vedi là, inizia così e c’ è la velocità, poi…”
Erik:
“ Si ferma,” e muove la mano verso l’ asse dei tempi disegnato da Irene.
Irene:
“ E va giù.”
Mattia:
“ E cosa ha fatto lui?”
Erik: “ Ogni gobba della velocità,” indica il grafico
in basso, “ è mezza lì,” addita quello in alto. Crea, quindi, una
corrispondenza fra i cambiamenti di concavità dei due grafici.(Quello della
velocità è stato disegnato da destra verso sinistra al contrario di quanto si
fa abitualmente.)
Espressione delle funzioni
contrattuale e di chiarimento dei linguaggi verbale e gestuale.
Quando
la calcolatrice produce il grafico, le facce di Irene, Erik e Mattia risultano
chiaramente stupiti. Parte della perplessità è dovuta al fatto che il grafico
presenta dei tratti in cui il valore della velocità è negativo.
PROF: “ Questo significa che stiamo considerando una
velocità negativa.”
Michele:
“ Ho la velocità minore quando è fermo, ma può esserci una velocità più
piccola di quella?”
PROF: “ Lo spazio è misurato qua,” addita il grafico
distanza-tempo, “ può mai essere negativo?”
Intervento in zona di sviluppo
prossimale, che stimola l’ evolversi del ragionamento in Paola e in Cristina.
Quest’ ultima giunge a formulare un’ ipotesi ben precisa a partire dai
ragionamenti dei compagni e dall’ analisi dei due grafici: dinamica
interno/esterno.
In
coro: “ No!”
Paola:
“ Solo se vado dietro il sensore.”
PROF:
“ Cerchiamo di dare un significato allo spazio negativo e alla velocità
negativa.”
Simone:
“ La velocità è negativa quando sta fermo.”
PROF:
“ Allora qui c’ è una contraddizione: se è fermo la velocità è zero.”
Irene:
“ Quando la velocità è costante e si ha una decelerazione.”
Secondo
Erik è impossibile che la velocità scenda sotto l’asse dei tempi.
PROF: “ Però succede, perché?”
La
calcolatrice come mezzo di rappresentazione della realtà.
Cristina:
“ La velocità scende quando mi avvicino al sensore.”
PROF:
“ Questa è un’ ipotesi ed è facile da verificare.”
Nuovo
intervento volto a suggerire la verifica sperimentale. Gli studenti però
preferiscono continuare a discutere e avanzano altre idee senza considerare a
fondo quella di Cristina. Soprattutto Michele inizia a produrre una serie di
ipotesi in modo molto confuso e a sostenerle veementemente, anche se con poca
forza dialettica e logica. La buona
idea di Cristina si perde e riemerge solo alla fine della mattinata, quando
l’insegnante obbliga quasi gli studenti a sottoporre all’esperimento le
molte idee che hanno messo in gioco, spesso in modo confuso. Non è chiaro agli
studenti che la confusione delle idee tende ad aumentare fino a livelli critici
quando non si hanno strumenti (o non li si vogliono usare) per sondare le idee
che via via vengono espresse. È
buona norma valutare le idee che vengono proposte prima di proporne altre:
l’unica eccezione si può fare quando si hanno due o tre posizioni ben
differenziate. La loro discussione parallela può portare grandi contributi alla
comprensione dei concetti interessati. Ma se l’attività si limita a proporre
nuove idee senza validare quelle già proposte, si fa poca strada.
Gianluca: “ No, è quando ci si avvicina al sensore
rispetto alla posizione di partenza.”
PROF:
“ Cioè rispetto alla velocità cambia se parto di qui e mi avvicino,”
inizia a muoversi dal punto più distante dallo strumento, “ o se parto di qui
e mi avvicino?” E avanza da metà aula.
Michele:
“ No, dipende dal punto di origine, se da qui vado avanti,” indica lo
spigolo della lavagna, “è negativa, se torno indietro mi allontano ed è
positiva.”
PROF:
“ Anche questa ipotesi è verificabile.”
Nuovo
intervento che suggerisce di verificare sperimentalmente.
Si cerca, quindi, un confronto diretto fra i due grafici
e il professore ribadisce che l’ asse dei tempi è il medesimo.
Azione di chiarimento.
Simone suppone che la presenza di velocità negative sia
dovuta ad un errore di valutazione della macchina a causa di un avvicinamento
eccessivo all’ oggetto (i ragazzi sono a conoscenza dei limiti di azione dello
strumento), ma il professore smentisce quest’ ipotesi, utilizzando il grafico.
Il grafico come strumento di
validazione.
Paola:
“ Perché non ci sono linee orizzontali nella velocità?”
PROF: “ Come si fanno le linee orizzontali nella velocità?”
Azione in zona di sviluppo
prossimale.
Paola:
“ Quando la velocità è costante.”
PROF:
“ Non è però facile ottenerla.”
Paola:
“ Ci sono però tipo delle rette,” addita il grafico spazio-tempo.
PROF:
“ Possono essere approssimate a rette, ma non lo sono.”
Secondo
Michele, un’ altra ipotesi è che la macchina, nel tracciare il grafico della
velocità, faccia un continuo confronto con la velocità iniziale. La sua idea
viene bocciata, perché la velocità iniziale è chiaramente zero.
PROF: “ Proviamo a fare delle prove per capire.”
La calcolatrice come strumento
per giungere a delle nuove congetture.
Va alla lavagna Michele: parte da in fondo alla classe e
avanza lentamente, torna indietro rapidamente, si ferma e ripete nuovamente la
stessa sequenza di azioni.
Viene
lasciato del tempo per consentire ai diversi gruppi di disegnare il grafico
relativo alla velocità, corrispondente ai movimenti di Michele.
Irene:
“ Non va sotto.” E disegna.
“
Per me fa così.”
Erik
invece disegna un altro grafico.
Mattia:
“Non continua a salire se no vuol dire che aumenta.”
Erik:
“ Arriva al punto massimo e poi si ferma.”
Il
risultato ottenuto con la calcolatrice è completamente diverso da quello che si
aspettavano i ragazzi, che appaiono sconfortati.
PROF:
“ Regge l’ ipotesi di Cristina? Per il primo tratto mi sembra che funzioni,
allora forse è vero che se mi avvicino ho delle
velocità negative e se mi allontano diventano positive,
indipendentemente dal punto di partenza.”
La calcolatrice come strumento di
validazione di un’ ipotesi.
Irene: “ Ma cosa centra lo spazio con la velocità? L’
avvicinarsi con la velocità? Cos’ è una velocità negativa?”
Lo sconcerto prodotto dalle
scoperte ottenute, precipita Irene nella crisi: perde contatto anche con le
intuizioni avute ad inizio esperienza.
Alessio
tenta una spiegazione dell’ azione del sensore: “ Mentre mi avvicino gli
impulsi che manda il sonar mi arrivano tutti contro il corpo e tornano indietro
tutti in un colpo, allora è logico che la velocità sia aumentata.”
PROF:
“ Non è vero, il sensore traccia il grafico della variazione di velocità.”
Michele: “ Forse la calcolatrice interpreta come velocità
negativa semplicemente quella che si avvicina, distingue la velocità del corpo
se si avvicina o se si allontana.”
Erik
non è d’ accordo.
Francesco:
“ Per me il sonar è tarato in modo tale che oltre una certa velocità lui
segna negativo comunque.”
La funzione programmatrice
consente l’ elaborazione di un’ infinità di ipotesi ed interpretazioni
possibili.
Il problema è che a mio
avviso qui manca un controllo delle ipotesi effettuate: la generazione di
ipotesi “alla Michele” assomiglia più alla generazione casuale di testi che
non alla costruzione razionale di ipotesi interpretative. Sembra che i ragazzi
(Michele soprattutto) sparino quello che viene loro in mente con la speranza di
dire qualcosa che interessi l’insegnante e che tale interesse suggerisca loro
qualche idea veramente buona.
PROF: “ Perché?”
Francesco:
“ Forse la segna negativa quando è più lenta.”
PROF:
“ Non sappiamo se quest’ ipotesi è vera, ma si può confutare
allontanandosi e vedendo se segna negativo o no.”
Altro
invito all’esperimento.
Irene:
“ Forse la velocità è in un certo senso anche la posizione.”
PROF:
“ L’ avvicinarsi e l’ allontanarsi.”
Azione di chiarimento.
PROF: “ Per darvi una mano a capire vi chiedo una cosa:
come la definite la velocità?”
In
coro: “ Spazio fratto tempo.”
PROF:
“ Ma spazio cosa vuol dire: lo spazio percorso o la posizione?”
Intervento in zona di sviluppo
prossimale.
Qualcuno: “ Lo spazio percorso.”
Il
professore conferma: “ In genere si usa questa scrittura ds/dt. Per sapere
quanto spazio ho percorso, valuto la differenza di posizione rispetto al sistema
di riferimento. Sono qui a 2 metri, mi avvicino e sono a 1 metro,” intanto
avanza, “allora ho percorso 2-1, 1 metro. Il tempo invece scorre solo in una
direzione, l’ istante finale è sempre maggiore di quello iniziale, va verso
il più e basta, quindi dt è sempre positivo. Per calcolare lo spazio percorso
in genere si fa lo spazio iniziale meno quello finale. Immaginate di partire con
me,” e va indietro, “ la posizione finale è maggiore o minore di quella
iniziale? Maggiore, allora se faccio se faccio posizione finale meno posizione
iniziale ottengo un numero…”
In
coro: “ Positivo.”
PROF:
“ Se parto di qui,” è in fondo alla classe, “ e mi muovo,” va avanti,
“la posizione finale è circa un metro, posizione finale meno posizione
iniziale è un numero negativo. Allora ds minore
di zero mi dice che mi sto avvicinando al sistema di riferimento, quindi sulla
velocità è importante sapere il verso in cui mi muovo. E’ l’ ipotesi di
Cristina quella che funziona.”
Intervento
di chiarimento nel quale si fa cenno agli schemi legati ai campi concettuali
assi cartesiani e sistema di riferimento.
Ma
quando la velocità cresce e quando decresce? Mentre vado indietro, mi muovo nel
senso crescente del tempo e dello spazio,” e intanto numera 1, 2, 3… “ se
invece parto di qui, e vado avanti faccio 4, 3, 2, 1.”
Dal
video si vede chiaramente che molti studenti alla fine capiscono come si può
interpretare una velocità negativa. L’idea di Cristina era buona, ma sembra
che nessuno la riconosca come idea di Cristina. Una buona idea si è persa per
strada, per l’abitudine a non sapere ascoltare e a non discutere le idee
proposte.