Il giorno successivo alla seconda esperienza con i sensori si è chiesto agli studenti di riflettere in piccoli gruppi sull’esperienza del giorno precedente. I vari gruppi hanno avuto come consegna (per il 14 gennaio) la preparazione di una relazione che si proponesse come obiettivo quello di spiegare a uno studente di terza media le relazioni esistenti tra spazio percorso, posizione rispetto a un determinato sistema di riferimento, tempo trascorso, istante rispetto a un determinato sistema di riferimento, velocità e accelerazione di un corpo in movimento (rispetto a un determinato sistema di riferimento). I vari gruppi di lavoro avevano la possibilità di iniziare a impostare la relazione nella lezione odierna e di verificare (o confutare) determinate ipotesi sulle relazioni esistenti tra la pendenza (o il tipo di curva) di un grafico spazio – tempo e la velocità e le sue variazioni nel tempo.

Come si può osservare, ogni componente del gruppo di lavoro ha un compito ben definito, che viene assegnato a rotazione. In questo caso Mattia è la "memoria del gruppo", ossia si occupa di stendere un diario di bordo delle varie strategie adottate dal gruppo per risolvere il compito e, in generale, dei problemi di carattere cognitivo, relazionale e affettivo sorti durante il lavoro. Erik è colui che è "orientato al compito"; si occupa, in altri termini, di verificare costantemente che il gruppo sta lavorando affettivamente al compito che è stato assegnato. Infine Irene è "orientata al gruppo"; il suo compito è quello di verificare costantemente che tutti i componenti del gruppo partecipino attivamente al lavoro, che non si verifichino fenomeni di emarginazione o di autoemarginazione. In un gruppo collaborativo è essenziale che ciascun componente abbia una responsabilità specifica che non sia solo quella di compiere una parte del lavoro, come invece può accadere in un gruppo cooperativo.

Osservazioni di Silvia  (in nero le osservazioni e i fatti; in rosso i commenti di Silvia)

LEZIONE DEL 18/12/2001

GRUPPO: ERIK, IRENE, MATTIA.

Memoria: Mattia

Orientato al compito: Erik

Orientato al gruppo: Irene

Il professore, inizialmente, cerca di chiarire una scoperta, che, nella lezione precedente, aveva lasciato gli studenti perplessi: il grafico relativo alla grandezza velocità può assumere valori negativi.

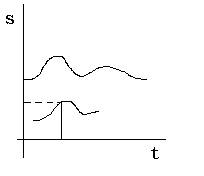
PROF: “ Consideriamo un grafico distanza-tempo e il corrispondente grafico velocità-tempo. Se prendo un punto che rappresenta 5 secondi e vado su, trovo il valore della velocità, per esempio 10 m/s.” Intanto disegna alla lavagna:

Azione della funzione di chiarimento, in cui viene recuperata la rappresentazione cartesiana della velocità.

“Cosa vuol dire 10 m/s? Che io sto percorrendo degli spazi tali che ogni secondo io percorro 10 m. Siccome non posso considerare dei tempi negativi, se no andrei indietro nel passato, e mi sto muovendo nella direzione positiva degli spazi, è chiaro che la velocità, che è il rapporto fra spazio percorso e tempo trascorso, sarà positiva, perché ho il rapporto fra 2 grandezze positive. Ma se io mi muovo e poi mi fermo, che velocità ho nell’ istante finale?”

In coro: “ Zero!”

Si attinge anche alla rappresentazione della velocità come rapporto fra spazio e tempo ed agli schemi legati al concetto stesso di rapporto.

PROF: “ Se adesso mi avvicino, ds, che è uguale a posizione finale meno posizione iniziale, è minore di zero, perché la posizione finale è inferiore a quella iniziale. Allora anche ds su dt diventa negativo, dipende semplicemente dalla scelta che io faccio di considerare crescenti quelle posizioni che ottengo allontanandomi dal sensore. Questo è il significato di velocità negativa. In sostanza si dice anche che la velocità è un vettore, si rappresenta con un vettore: non basta dire mi muovo a 100 km/h, ma devo dire anche in quale direzione e con quale verso.

Introduzione del concetto di vettore, la cui messa a punto viene ottenuta con riferimento a situazioni reali.

Se io dico “ Ieri sono andato a 100 km/h,” lui,” indica uno dei ragazzi, “ mi dice “Dove?” “ A Genova.” E lui mi dice “ Da dove, da Finale a Genova?” Allora devo considerare la direzione, cioè la  retta in linea d’ aria che congiunge punto di partenza e punto di arrivo e dire quale dei 2 estremi della retta è la partenza e quale l’ arrivo. Abbiamo così interpretato la velocità negativa.”

Viene quindi specificato lo scopo della lezione odierna: lasciare tempo ai diversi gruppi per preparare una relazione. Nell’esposizione si dovrà spiegare, a un ipotetico ragazzino di terza media, il lavoro compiuto utilizzando il sensore di moto e si dovranno descrivere i risultati così ottenuti.

PROF: “ Potete partire dagli esempi o dalla teoria sistemata. Ricordate, comunque, che state parlando ad un bambino di terza media e quindi il linguaggio dovrà essere per lui comprensibile.”

ERIK: “ Cosa dobbiamo spiegare?”

MATTIA: “ Tutta quella roba lì.”

IRENE: “ Le relazioni fra spazio, velocità, tempo…..”

ERIK: “E che relazione c’è?”

IRENE: “ Come che relazione c’è! E’ tutto quello che abbiamo fatto ieri.”

MATTIA: “ Ma come lo imposti? Ti fai la scaletta?”

ERIK: “ Ma abbiamo a disposizione la macchinetta?” E indica il sensore.

Per ERIK la relazione spazio-tempo è ottenibile solo grazie al sensore, non è possibile darne una spiegazione in modo diverso. Soltanto l’utilizzo dello strumento può portare alla deduzione del legame che esiste dal punto di vista grafico fra queste due grandezze.

IRENE: “ No, devi spiegare.”

ERIK: “ Perché se avevi la macchinetta, prima facevi l’ esempio e poi lo spiegavi.”

IRENE: “ Però è un ragazzo di terza media…inizi col dire cosa abbiamo fatto con la calcolatrice e col…radar…sonar.”

ERIK: “ Non centra niente il sonar.”

ERIK focalizza l’attenzione sul vero argomento della relazione da elaborare, che non è il funzionamento del sonar, ma i risultati che mediante esso si sono ottenuti.

IRENE: “ Serve perché parti da quello per arrivare a dire che…”

ERIK: “ Come ci arrivi?”

IRENE: “ Abbiamo gli esempi pratici.”

ERIK: “ Ma non la macchinetta.”

E’ ancora ribadita l’ importanza dell’ utilizzazione del congegno di supporto all’ esperienza, gli esempi pratici, secondo ERIK, non bastano a convincere un ascoltatore delle scoperte fatte. L’ esperienza diventa strumento deduttivo e così il sensore, il loro uso può sopperire alla spiegazione che non si riesce a dare a parole.

IRENE: “ Glielo spieghi.”

ERIK: “ Devi insegnargli ad interpretare il grafico?”

IRENE: “ No, è lo strumento per spiegargli cos’ è lo spazio, il tempo e le relazioni.”

ERIK: “ Cosa vuol dire relazione?”

IRENE si irrita nei confronti di ERIK.

MATTIA fa, quindi, un piccolo riassunto delle cose di cui sarà necessario parlare: i grafici, la velocità negativa, il funzionamento del sensore.

Espressione della funzione di chiarimento.

Il professore richiama l’ attenzione generale per rispondere a una domanda di uno degli altri ragazzi: “ Come si misura la pendenza? E’ il rapporto fra quanto si sale e quanto si va in orizzontale, cioè fra ordinate ed ascisse.”

Azione di chiarimento in zona di sviluppo prossimale.

ERIK: “ E poi parliamo anche delle curve.”

MATTIA: “ Quella così,” disegna un arco di parabola, “ è un’ accelerazione.”

ERIK: “ Prima devi spiegargli come si fa il grafico…”

MATTIA: “ Sulle ascisse hai…”

ERIK: “ Spazio, tempo.”

Il grafico cartesiano come rappresentazione di grandezze.

MATTIA: “ Ma c’è anche velocità-tempo. Velocità-spazio si può fare?”

ERIK: “ Puoi, ma non serve a niente.”

IRENE: “ Per me dobbiamo fare una specie di… introduzione.”

MATTIA: “ Sì, gli dici perché stiamo parlando di questa roba qui.”

IRENE: “ Gli dici che abbiamo usato quello strumento lì, per mettere in pratica le relazioni fra spazio e tempo.”

ERIK: “ E lui capisce! Ti chiede qual è la relazione e tu poi prova a rispondere!”

Uno dei ragazzi della classe effettua una prova col sensore e il gruppo cerca di fare una previsione sull’ andamento del grafico velocità-tempo corrispondente. Per sapere se le idee che si sono costruiti in merito all’ individuazione di velocità negative sono valide, anche MATTIA chiede di poter usare il sensore e concorda con i compagni i movimenti che dovrà effettuare.

ERIK: “ Vai indietro, ti fermi, vai indietro, ti fermi,…”

IRENE: “ Sì, ma fermati un po’.”

Vogliono produrre un grafico in cui la velocità assuma solo valori positivi. La calcolatrice è utilizzata come strumento di validazione.

Il professore suggerisce di produrre dei grafici spazio-tempo semplici, in modo che confutare o validare le proprie ipotesi sia più facile.

Il grafico spazio-tempo ottenuto da MATTIA è il seguente

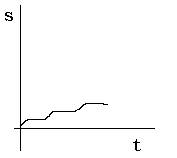
MATTIA disegna autonomamente quello della velocità associato e riesce a descriverlo correttamente.

Fatto ciò, tornano al lavoro iniziale.

IRENE: “ Spieghiamo le curve: così è costante,” disegna una retta uscente dall’ origine degli assi.

ERIK: “ No, deve essere così, perché un minimo di accelerazione c’è sempre.” Traccia

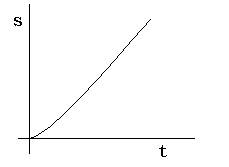
IRENE: “ Così è piano e si avvicina al sonar.” Descrive un arco di parabola con concavità rivolta verso il basso.

ERIK e MATTIA sottopongono IRENE a una sorta di interrogatorio.

ERIK: “ E se faccio così?”

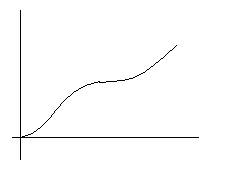
IRENE: “ Vuol dire che è partito forte, ha accelerato, ed è ripartito piano.”

MATTIA: “ E questo qua vuol dire?” Disegna una retta parallela all’ asse x.

IRENE: “ Che è sempre fermo.”

I ragazzi stimolano vicendevolmente i compagni a progredire in zona di sviluppo prossimale.

Il professore si intromette nella discussione ponendo alla classe la seguente domanda: è possibile che un corpo abbia velocità nulla e contemporaneamente non sia fermo?

Azione del professore in zona di sviluppo prossimale, che non è colta dal gruppo.

Qualcuno risponde che una situazione potrebbe essere quella in cui saltello su me stesso.

ERIK smentisce tale possibilità asserendo che anche così si avrebbe una certa velocità.

Il gruppo, quindi, si estranea dal problema e continua a discutere, isolatamente, sul grafico che ERIK proverà a produrre.

ERIK: “ Secondo te, per fare così cosa devo fare?” Disegna una funzione sinusoidale che mantiene sempre lo stesso periodo, ma la cui ampiezza, dopo un certo tempo, è incrementata.

IRENE: “ Parti, ti allontani, ti avvicini.”

ERIK: “ Piano però, perché la velocità dipende dalla pendenza.”

Alle varie rappresentazioni della velocità si è aggiunta anche la pendenza relativa ad un grafico spazio-tempo.

Paola, utilizzando il sensore, ottiene un grafico della velocità che non parte da zero, ciò stupisce IRENE.

PROF: “ Succede così perché parte già in moto, cioè con velocità diversa da zero.”

Intervento chiarificatore.

Il professore ripropone, quindi, la domanda di prima sulla possibilità di avere un corpo in moto con velocità nulla: “Pensate a quando si gioca a pallacanestro, quando il pallone passa per la velocità zero?”

Azione in zona di sviluppo prossimale con riferimento ad una situazione reale, che produce in IRENE una reazione. La realtà è ancora ambito di deduzione.

IRENE: “ Quando cambia direzione e quindi lì hai un moto con zero velocità.”

PROF: “ E’ meglio dire quando cambia verso.”

Espressione della funzione di chiarimento.

IRENE cerca di spiegarlo ai compagni utilizzando il banco in modo che rappresenti il pavimento e ponendo la mano sinistra orizzontalmente, ad una certa altezza, con l’altra mano simula l’ andamento della palla.

Il linguaggio gestuale è indispensabile per sopperire alle lacune della funzione di chiarimento.

ERIK chiede ad IRENE di disegnare un grafico spazio-tempo in modo che lui possa elaborare quello della velocità.